Theories of Failure (Failure Theories) – Popular in Strength of Material (SOM)

In the field of Strength of Materials, there are several theories that attempt to explain and predict the failure of materials under stress. By understanding these theories of failure in Strength of Materials, engineers can predict the behaviour of materials under stress, improve the design and performance of structures and components, and ensure their safety and reliability.

___________________________________________________

➲ Author – Jagadish Atole (Mentor at DesignGkez)

___________________________________________________

➲ Some of the popular failure theories are categories as: –

1. Maximum Principal Stress Theory:

This theory is also known as Rankine’s theory and states that “when a component is subjected to biaxial or triaxial state of stress, its failure occurs when the maximum principal stress reaches the yield strength or ultimate strength of the material.”

➲ Study in depth: https://youtu.be/RzCjMOOfOK0?si=euxc5ihuVGilRfez

2. Maximum Shear Stress Theory:

This theory is also known as Coulomb – Guest – Tresca’s theory and it states that “when a component is subjected to biaxial or triaxial state of stress, its failure occurs when the maximum shear stress at any point in the component reaches the maximum shear stress in the standard specimen in a simple tension test when yielding begins.” In short, we can say failure will occur when the maximum shear stress exceeds the shear stress at uniaxial loading.

➲ Study in depth: https://youtu.be/cuxBv-TFbyc?si=OEf7NW71divVU856

3. Maximum Principal Strain Theory:

This theory is also known as Saint Venant’s theory and it states that “the failure of a material will occur when the maximum value of principal strain developed in the body exceeds the value of strain corresponding to the yield point of the material.”

➲ Study in depth: https://youtu.be/T7yeb9-232w?si=pEZ0_k3XcBUEqb0N

4. Total Strain Energy Theory:

This theory is also known as maximum strain energy theory OR Haigh’s theory and it states that “the failure of material or component will occur when the maximum value of strain energy per unit volume exceeds the limiting value of strain energy per unit volume.”

➲ Study in depth: https://youtu.be/cDKloaaFN8k?si=xZdFfIF-2W4Xn8jN

5. Maximum Shear Strain Energy Theory:

This theory is also known as maximum distortion energy theory OR Hencky – Von Mises theory and it states that “the failure or yielding will occurs at a point in a member when the distortion strain energy per unit volume in a biaxial or triaxial stress system reaches the limiting distortion energy per unit volume as determined from simple tension test.”

➲ Study in depth: https://youtu.be/cDKloaaFN8k?si=lawykhuJVvkr59h_

_______________________________________________________

We know that when we apply the load on an object like the bracket (as shown in fig.1-a). Suppose initially we apply the load of some amount which this bracket can sustain without failure or without deformation (as shown if fig.1-b). Then if we keep on increasing the magnitude of a load, then at some point, the bracket will fail (as shown in fig.1-c).

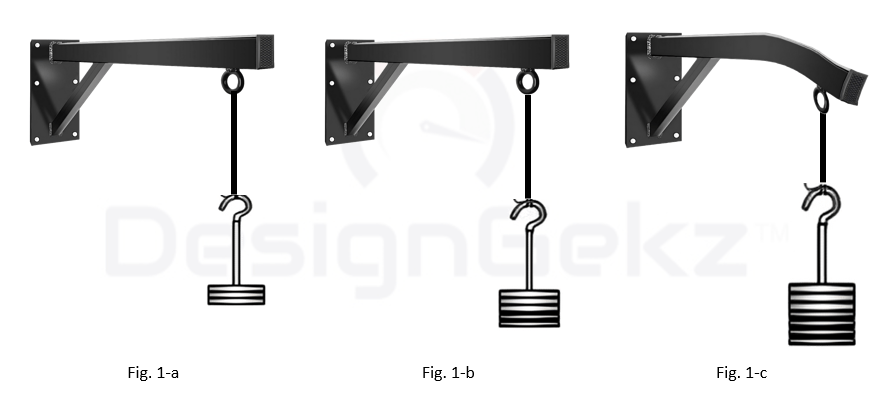
So how can we predict that when the failure will occur? Or what amount of maximum load the bracket can withstand? Or when the object will fail? Or what level does the stresses in the part need to reach it to fail?

The answer is “the part fails when the induced stresses exceed their strengths” means when we stressing the part beyond its strength then the part will fail. But what is failure? What means failure in the part or component? And what causes it to fail?

We can say part failed if it gets broken into two or more pieces (as shown in fig.2-a) or if the part gets deformed permanently that means permanent deformation (as shown in fig.2-b). Failure can be considered if the parts reliability downgraded or if the parts function compromised.

So, to prevent failure, we must know that what causes the failure.

The failure depends on the kind of stresses like tensile or compressive stresses due to axial load or bending load. Or shear stress due to torsion or transverse shear.
Essentially failure depends on materials relative strength in tension, compression and shear.
Failure also depends on the type of loading like – static, fatigue and impact.
It also depends on the presence of cracks in the component.

So, if design engineer speaking of failure can mean any or all of these possibilities. In short, the part or component is said to have failed if it becomes unsuitable for performing its desired function.

(Fig 3-a & 3-b)

Some examples of such components are like I.C engine crankshaft, shaft used in power transmission & other shafts, bolted & welded joints used under eccentric loading (as shown in fig.3-a) or the spindle of screw jack or screw jack components or crane hook & crane components (as shown in fig.3-b), where the failure may occur due to excess induced stresses or whatever the reason leading to failure & part or component will not perform its function properly or it may not serve its function for which it is designed.

Basically, there are two types of mechanical failure, first is yielding and second is fracture.

The yielding results in excessive permanent deformation which makes the part unfit to perform its function satisfactorily. This yielding or elastic failure (as shown in fig.4) mostly occurs in ductile materials, means for ductile materials, failure is usually considered to occur at the onset of plastic deformation.
On the other hand, the fracture (as shown in fig.4) results in breaking the component into two parts. This fracture mostly occurs in brittle materials, means for brittle materials, failure occurs at fracture.
In some applications where the components are desired to have sufficient rigidity, the excess elastic deformation, even if its not permanent, could be the reason for failure to perform desired function.
There is no sharp line of demarcation between ductile and brittle material fracture. However, a rough guideline is that if the percentage elongation is greater than 5% then the material may be treated as ductile material and if the percentage elongation is less than 5% then the material is treated as brittle material.
However, there are many instances when a ductile material may fail by fracture which may occur if a material is subjected to cyclic loading or long-term static loading at elevated temperature, due to impact loading, weak hardening or due to severe quenching also.
In general, ductile materials or isotropic materials are limited by their shear strengths and ductile materials are limited by their tensile strengths.

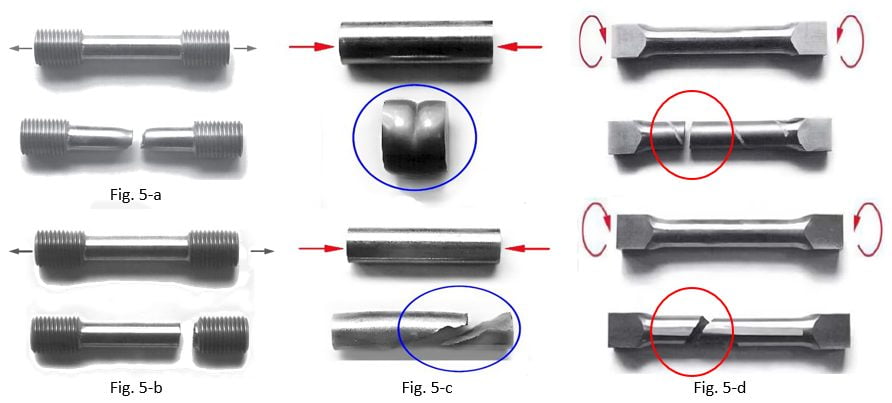
In the fig. 5-a you can see the tensile test specimen of ductile steel. The failure is occurring along principal shear stress plane. The fig.5-b is the result of tensile test specimen of brittle steel. In this the failure is occurring along principal normal stress plane. The test results of ductile and brittle material will vary under compression. In fig.5-c the test results of compression test specimen of ductile steel and brittle cast iron is shown. In compression test, the ductile steel gets deformed and brittle cast iron gets fracture. In torsion test, the ductile steel specimen fracture and brittle cast iron specimen fracture is shown in fig.5-d.

Now, let’s discuss Why do we need different failure theories?

As we discussed earlier that for ductile materials, the failure is usually considered to occurs at the onset of plastic deformation and for brittle materials it occurs at fracture. These points are easy to define for uniaxial stress state like a tensile test and can be plotted on stress strain curve (as shown in fig.6) It occurs when the normal stress in the object reaches the yield strength for ductile material and the ultimate strength for brittle material.

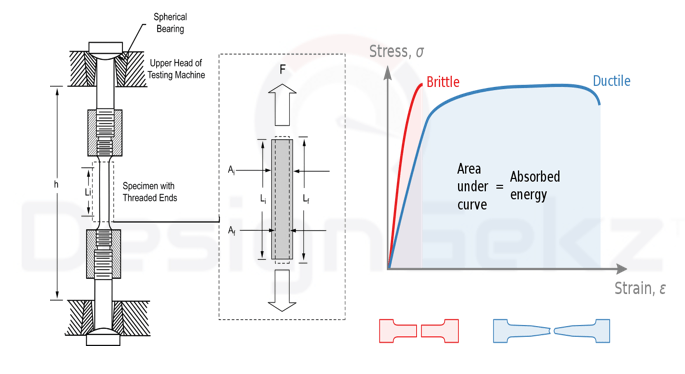
In short, for a machine part subjected to uniaxial system of stress that is , the limiting allowable stress for the design may be obtained from the simple tension test where usually the yield point stress is the deciding factor in uniaxial system of stress condition. But in majority of cases, the parts are subjected to complex stress system.

So, in case of multidimensional stress at a point (as shown in fig.7-b), we have more complicated situation present. Since it is impractical to test every material and every combination of stresses that is and , the failure theories are needed for making the predictions on the basis of materials performance on the tensile test of how strong it will be under any conditions of static loading.

Different scientist gave relationships between stresses induced under combined loading conditions of yield strength and ultimate strength obtained using tension test which are called theories of failure. We have different theories of failure like:

Maximum principal stress theory also known as Rankine’s theory for brittle material such as cast iron.
Maximum shear stress theory or Coulomb – Guest – Tresca’s theory for ductile material like in case of shaft.
Maximum principal strain theory also known as Saint Venant’s theory, which is suitable for both ductile and brittle material.
Strain energy theory or Haigh’s theory. This theory is also known as maximum strain energy theory and it is applicable for ductile material particularly in case of pressure vessel.
Maximum distortion energy theory or Von Mises & Hencky’s theory which is suitable for ductile material particularly in case of pure shear.

The failure theories which apply for ductile materials usually are not applicable for brittle materials and vice-versa. And the theory behind the various failure theories is that whatever is responsible for failure in the standard tensile test will also be responsible for failure under all other conditions of static loading.

➲ What does the failure theory do?

These failure theories help in finding out the load capacity of a component.
It allows us to predict failure of a material by comparing the stress state in the object with material properties like yield or ultimate strength obtained by performing uniaxial tensile test.
It gives or it establish the relationship between the ultimate tensile strength and yield strength.
σ_yis the yield strength for ductile material and σ_uis the ultimate strength for brittle material.
In case of ductile material, the failure occurs at plastic deformation and for brittle material, the failure occurs at fracture.

The stress state at a point can be described using the three principal stresses so most failure theories are defined as a function of the principal stresses and the material strength.

F (σ1, σ2, σ3) = σ_y, σ_u

The failure occurs when the maximum or minimum principal stresses reach the yield strength or ultimate strength of the material.

By convention, principal stresses are ordered from largest to smallest as σ1 ≥ σ2 ≥ σ3

At yield point in tension test, the maximum principal stress is equal to yield strength of the material and the other two principal stresses are equal to zero i.e. σ1 = σyt, σ2 = 0, σ3 = 0

For generally used ductile metals, yield strength in tension is equal to yield strength in compression i.e.

σyt = σyc

_____________________________________

⏩ Read my other blogs to understand top mechanical design skills for 10X career growth.

⏩ Read blog: https://designgekz.com/most-in-demand-skills-in-mechanical-design-engineering/

__________________________________________________

⏩ For career planning or enquiring about the courses, write to us at kevinkutto@designgekz.com or call us @ +91-8329029492 | 9881521371

__________________________________________________

⏩ Learn most in demand mechanical design skills like Plastic | Sheetmetal domains, NPD | NPI Process, DFMEA, GD&T (Basic & Pro), PPAP, Tolerance Stackup Analysis, Value Engineering and more with our Signature mentorship Program – Master Diploma in Plastic & Sheetmetal Design Professional (PSDP):